Adaptive Bayesian Filter Implemented in FPGA for Performance Improvement of Low-Cost Sensors
Gabriel Shimanuki, Rafael Yokowo, Alexandre Nascimento, Lúcio Vismari, Paulo Cugnasca
Abstract: Distance sensors are commonly used for obstacle detection and distance measurement, providing information for various applications such as collision prevention, object detection, and terrain mapping. However, they exhibit a wide range of quality and accuracy, with prices ranging from USD 0.55 to over USD 100 per unit. Choosing the lowest-priced sensors directly impacts the reliability of the measurements, as noise levels in the measured values can be significant. This project aims to present an adaptive Bayesian filter model as a proof of concept to improve the reliability of measurements from low-cost sensors.
Introduction
The developed project aims to present a proof of concept for the application of a Bayesian Filter in FPGA to enhance the reliability of measurements taken by the HC-SR04 ultrasonic sensor. The prototype is built by assembling a circuit using the VHDL hardware description language and Intel Quartus Prime, which implements the solution proposed in Nascimento et al. (2018), with necessary and convenient adaptations for the FPGA project. The model is based on a series of Bayesian networks (or Hidden Markov Chains).
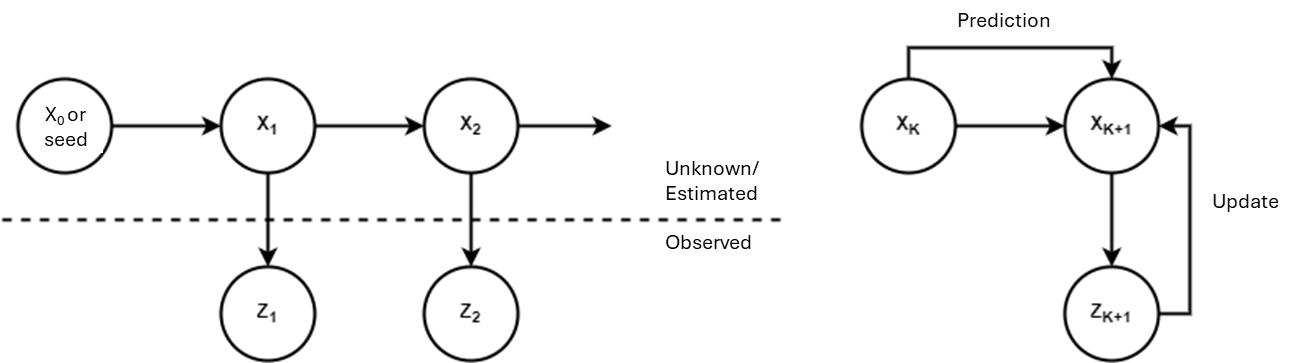
Figure 1: Bayesian Network Model (left) and Prediction Update (right)
Technical Solution
In this project, floating-point calculation modules (IEEE 754) were developed to implement the Bayesian filter in hardware, a module for converting the sensor measurements to floating point, and a module for controlling the adaptation of the Bayesian filter. The calculation module was responsible for implementing the main expressions that make up the Bayesian filter (described in [1]), which will be presented below:
\[k_{k|1} = \left(\frac{\sigma_k^2 + \sigma_p^2}{\sigma_m^2 + \sigma_p^2 + \sigma_k^2}\right) \tag{1}\] \[\sigma_{k|1}^2 = (1 - k_{k|1})(\sigma_k^2 + \sigma_p^2) \tag{2}\] \[x_{k|1} = k_k z_{k|1} + (1 - k_{k|1})x_{k} \tag{3}\]with the following initial conditions:
\[k = \left(\frac{\sigma_0^2 + \sigma_p^2}{\sigma_m^2 + \sigma_p^2 + \sigma_0^2}\right) \tag{4}\] \[\sigma_{1}^2 =(1 - k_{1})(\sigma_0^2 + \sigma_p^2) \tag{5}\] \[x_{1} = k_1 z_{1} + (1 - k_{1})x_{0} \tag{6}\]Let \(x_0\) be a seed value and \(\sigma_0^2\) an arbitrary value to start the iterations. The outputs or estimates of the model, denoted by \(X_{k \vert 1}\), are given by \(X_1 = X_0 + \epsilon_P\) with \(\epsilon_P \sim N(0, \sigma_p^2)\). In turn, the measured distances are represented by the true measured value with added uncertainty given by \(\sigma_m^2\).
The development of these calculation components and the conversion of the sensor signal, specifically the floating-point arithmetic components, was supported by the libraries available in the Intel Quartus development software – IP Catalog.
The circuit is capable of performing distance measurements from the ultrasonic sensor, executing the Bayesian filter calculations, and transmitting both the measured and filtered data to a Python-based notebook interface via serial communication and MQTT protocol. Finally, the adaptive control module allows adjustments to the sensor parameters, altering the sensitivity of the filtering.
Results and Discussion
Through the proposed solution, it was possible to obtain very satisfactory results, achieving different operational conditions of the filter in which the adaptation to the environment is variable. Three distinct filtering tests will be presented. Figures 2 and 3 show tests with fixed parameters. In Figure 4, the filtering performed is the result of the automatic adaptation of the circuit, as shown in Table 2.
- Case 1: Variance comparison with fixed parameters:
- Measured Variance: 926.11 mm²
- Estimated Variance: 780.54 mm²
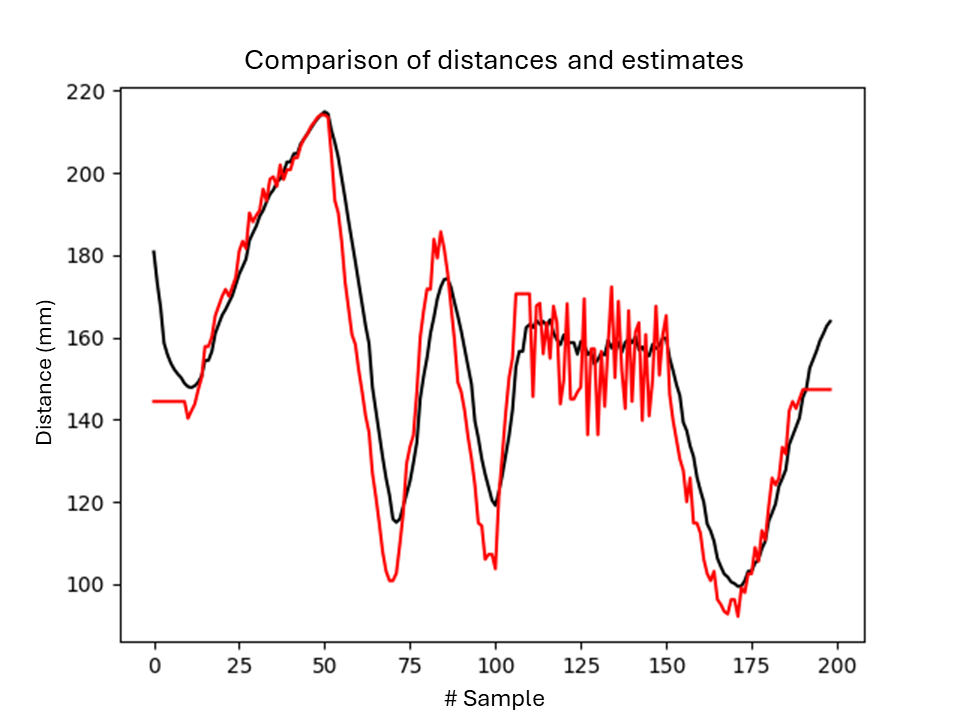
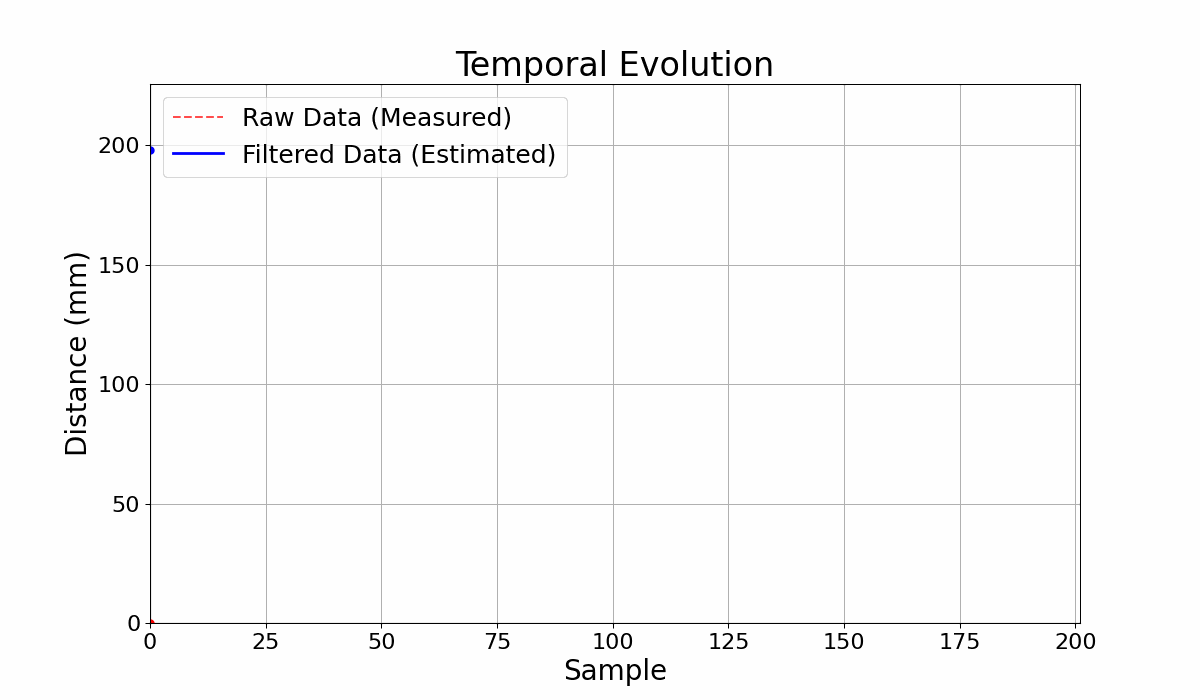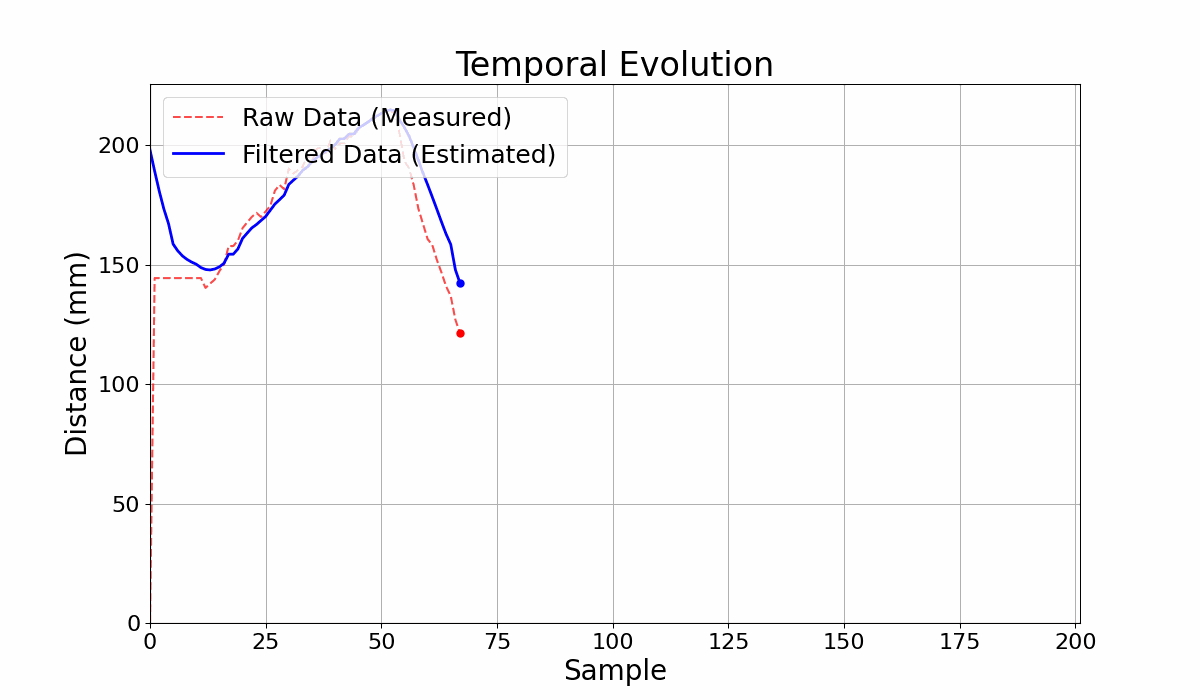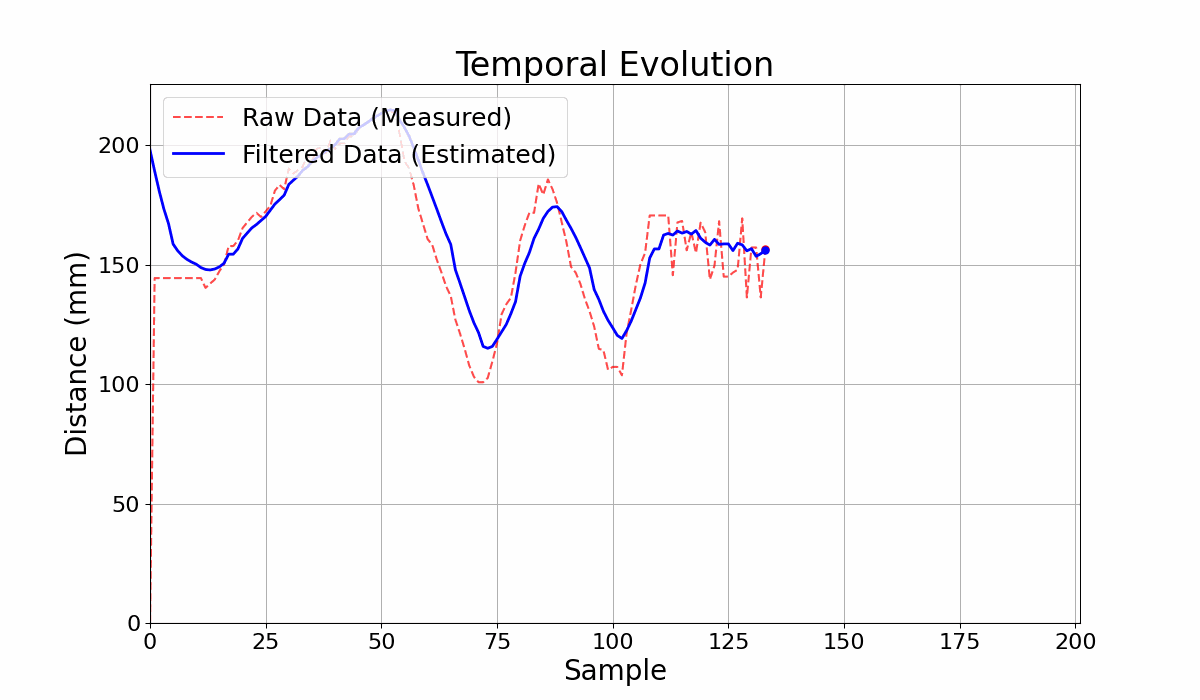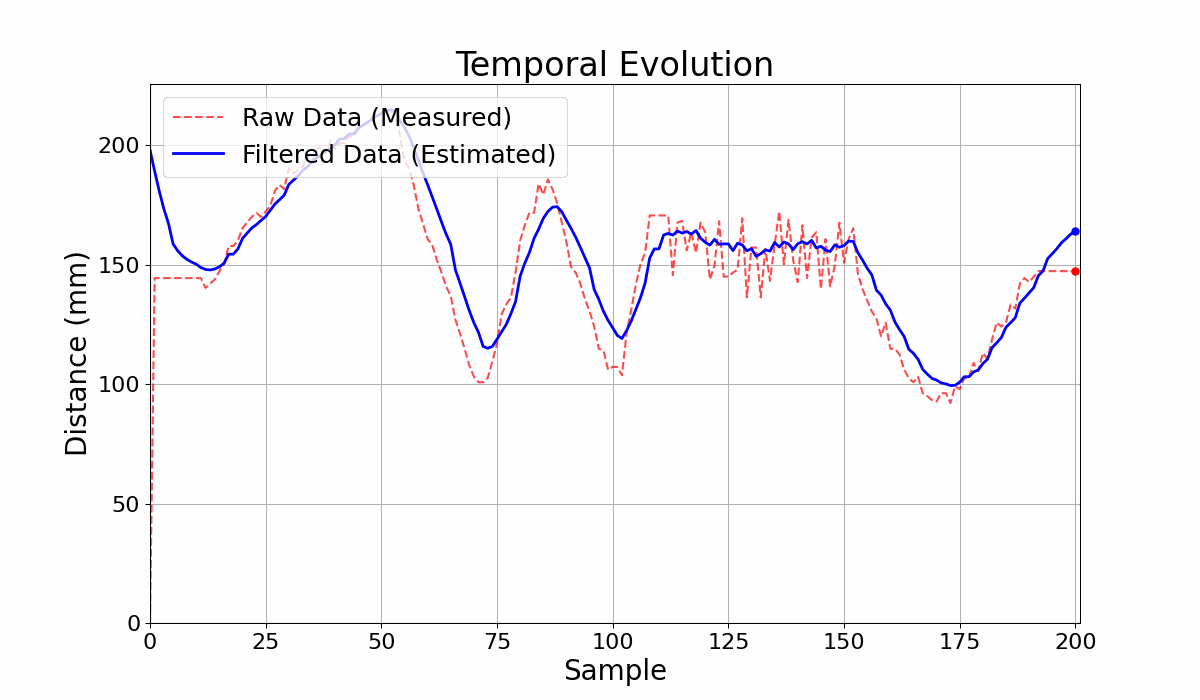
Figure 2: Output Comparison for the Circuit with filter and without filter.
- Case 2:
- Measured Variance: 732.69 mm²
- Estimated Variance: 713.32 mm²
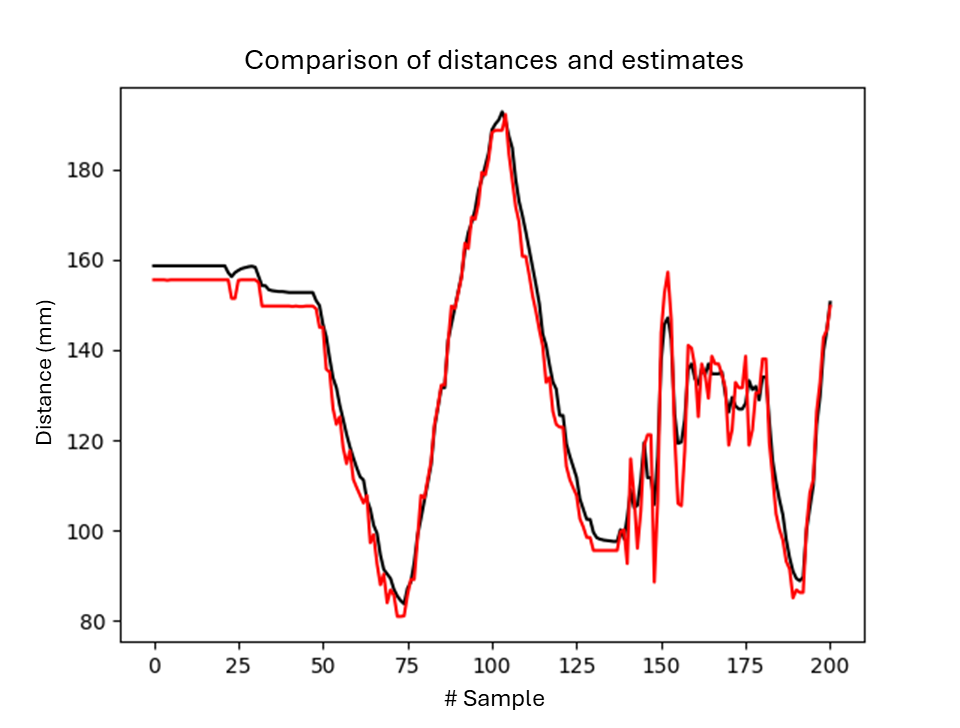
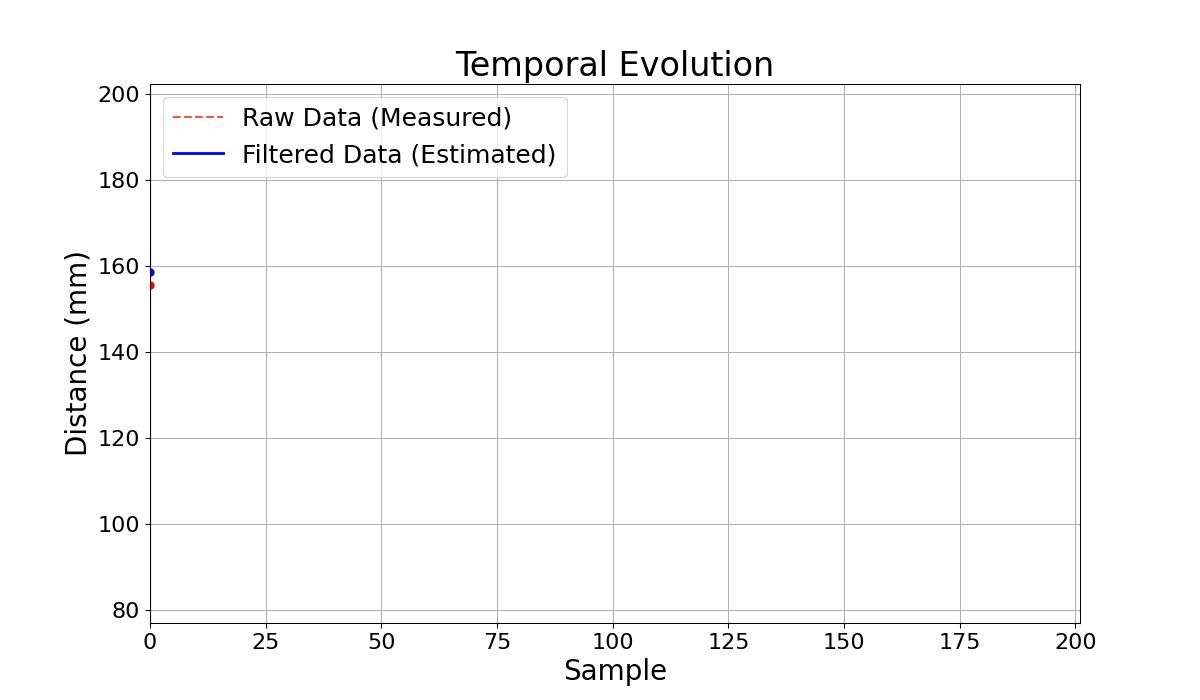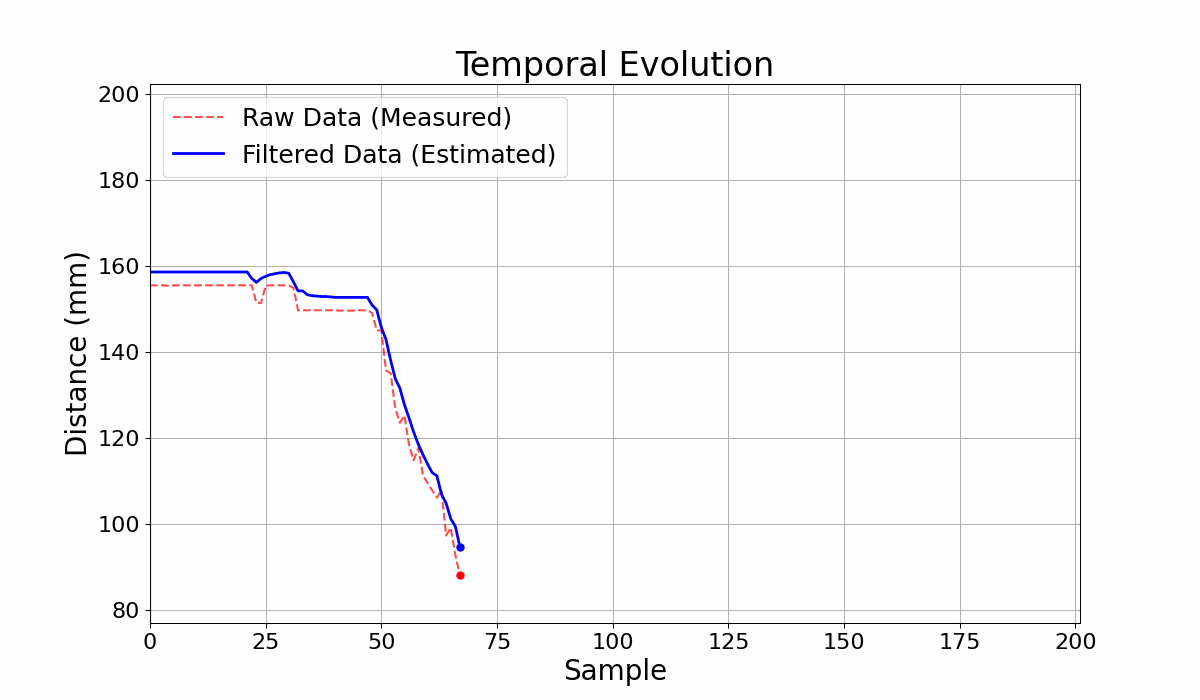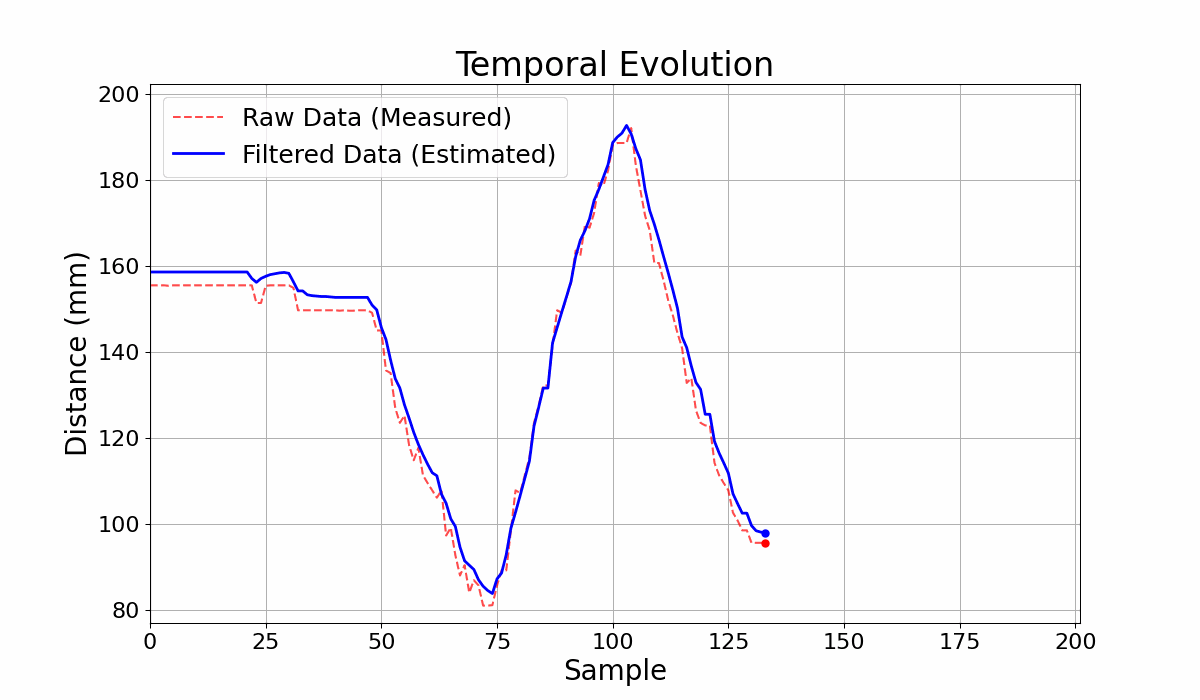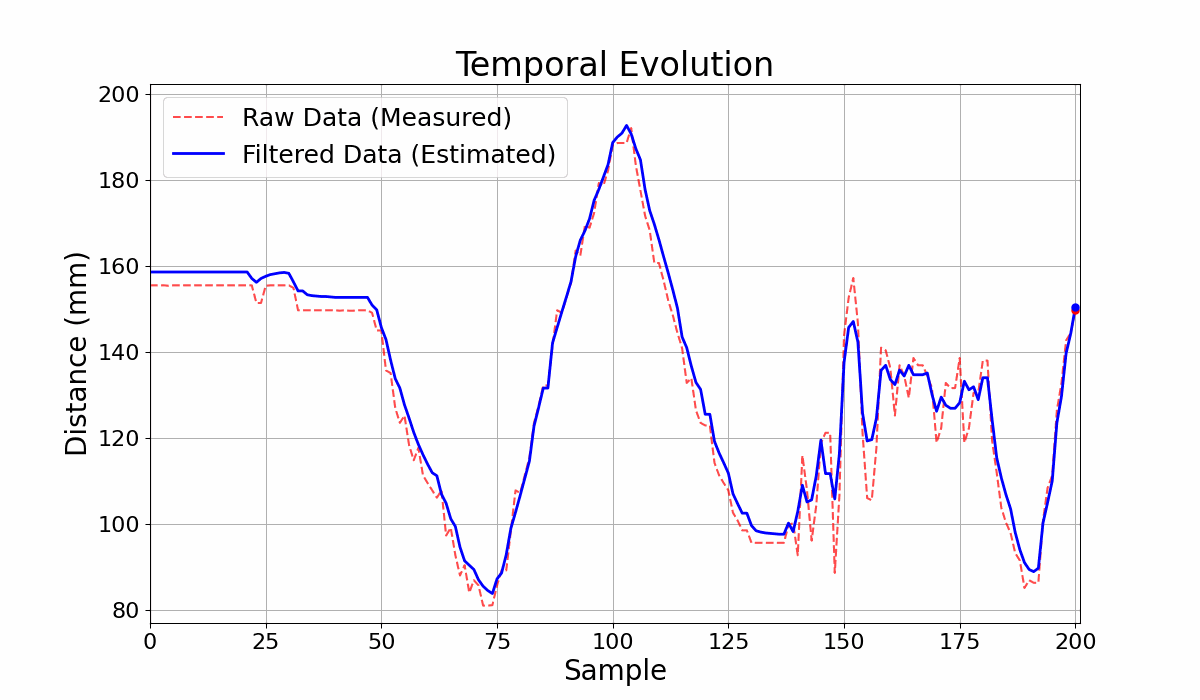
Figure 3: Output Comparison for the Circuit with filter and without filter.
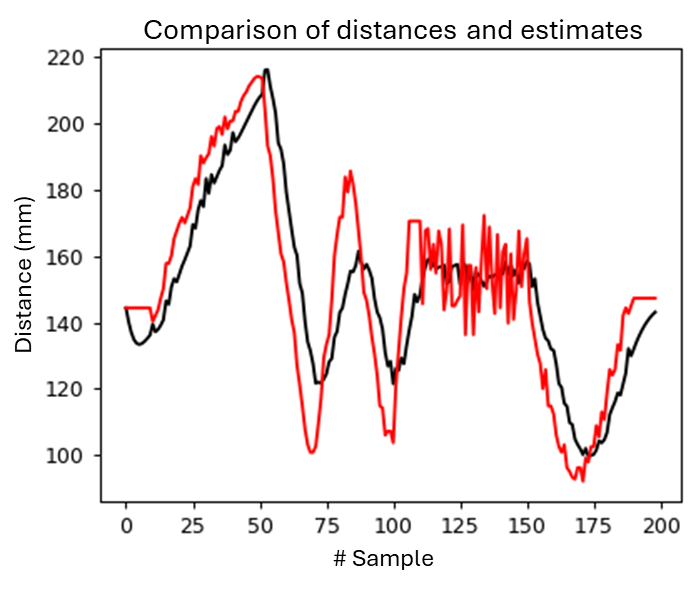
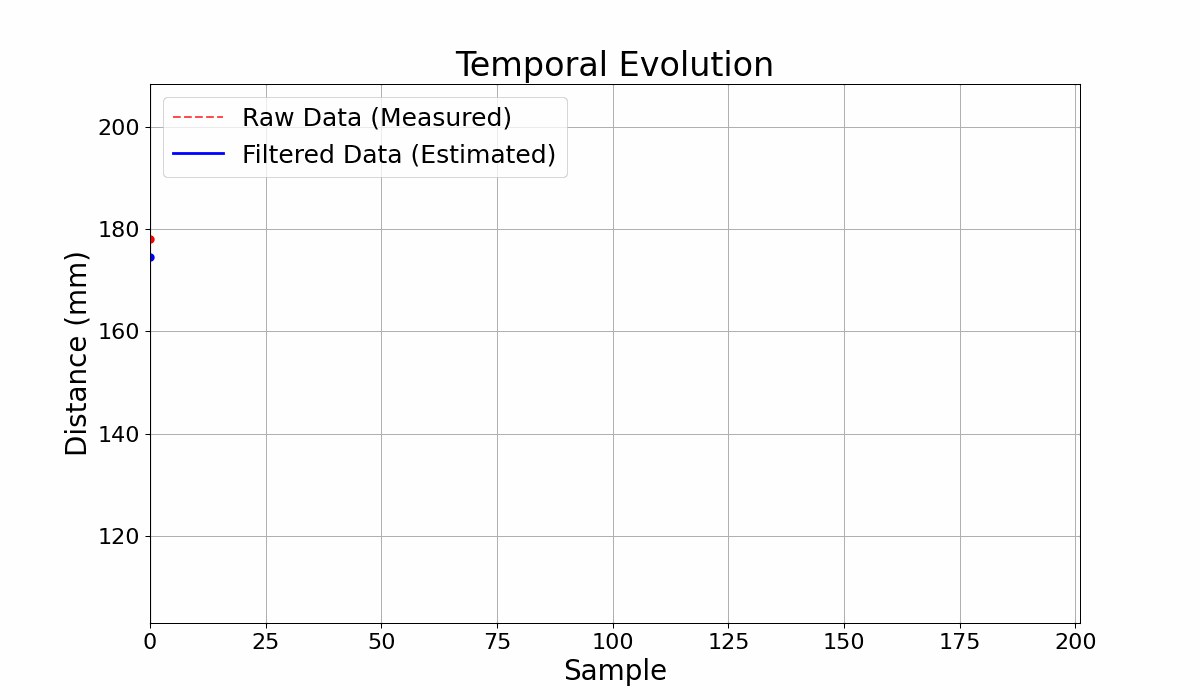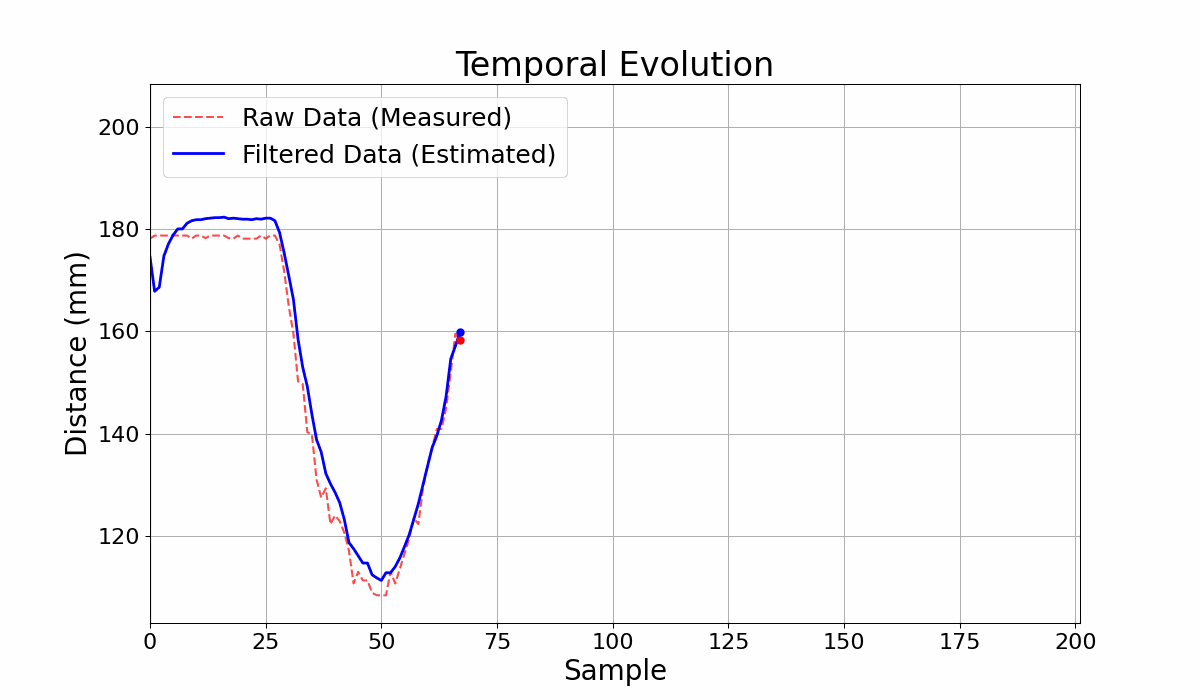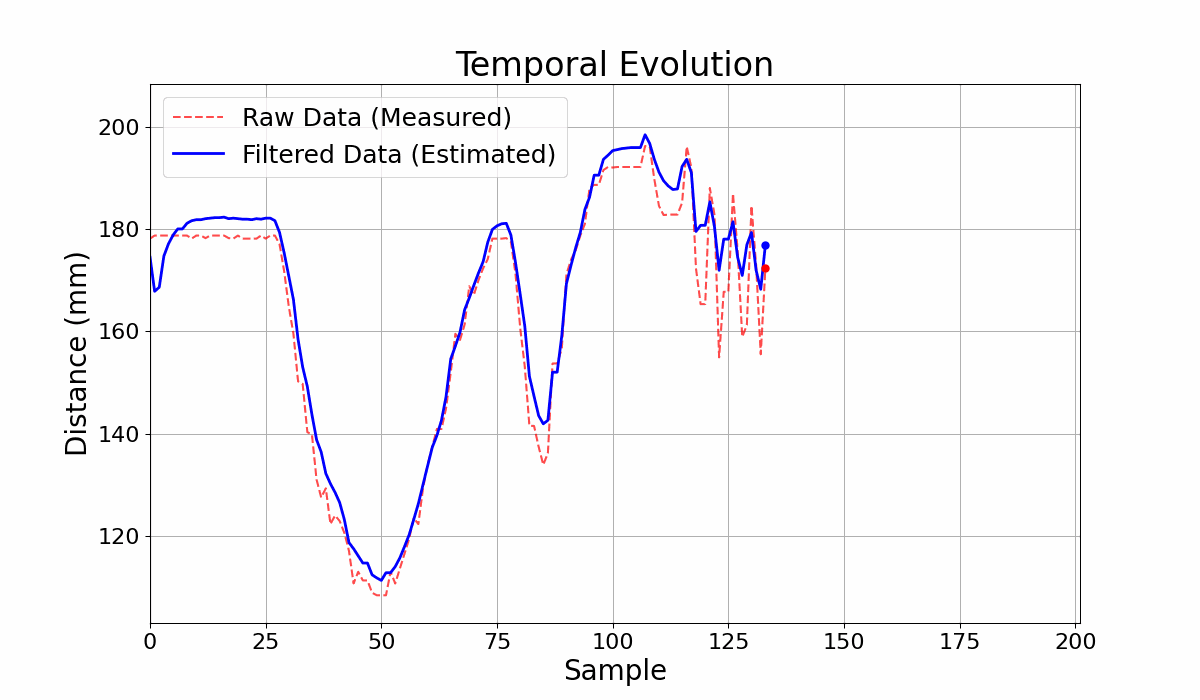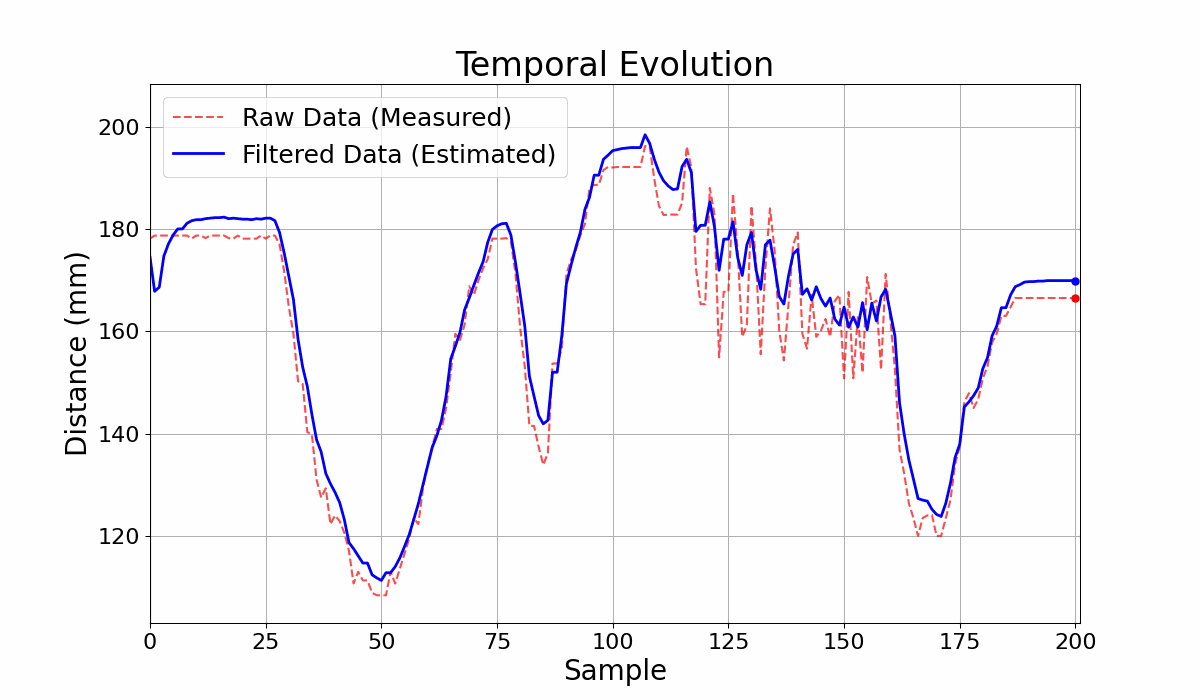
Figure 4: Output Comparison for the Circuit with filter and without filter - Adaptive Circuit.
Thus, the following variances were obtained, where the real variance represents the measurements from the standard circuit and the estimated variance represents the measurements from the circuit with the filter applied.
Adaptive Filtering
The adaptive model improved noise filtering:
- Measured Variance: 926.11 mm²
- Estimated Variance: 694.80 mm²
| Case | Measured Variance | Estimated Variance |
|---|---|---|
| Case 1 (Fixed) | 926.11 mm² | 780.54 mm² |
| Case 2 (Fixed) | 732.69 mm² | 713.32 mm² |
| Adaptive Case | 926.11 mm² | 694.80 mm² |
Table 1: Comparison of variances between the measured and estimated curves.
| Intervals (Accel in unit U) | \(\sigma_{P}\) | \(\sigma_{M}\) | Address |
|---|---|---|---|
Acel > 10 |
0.01 |
0.6 |
000 |
7 < Acel < 10 |
0.05 |
0.6 |
001 |
3 < Acel < 7 |
0.08 |
0.58 |
010 |
0 < Acel < 3 |
0.1 |
0.55 |
011 |
Table 2: Addressing relation of the parameters.
The filtering parameters of the Bayesian network yield different results depending on the sequence of measure- ments to be filtered. In Figure 3, for example, the good cou- pling between the curves in the measurement range from 0 to 125 results in ineffective noise filtering for the range from 130 to 180. The adaptive filtering model is an alternative to improve noise filtering. In Table 1, the first and third rows show the results of filtering the same set of measure- ments. The variance obtained with the adaptive model was lower, indicating preliminary better filtering. However, in this case, the lower variance resulted in a worse coupling between the curves, as seen in Figures 2 and 4.
Conclusion
The project successfully implemented an adaptive Bayesian filtering circuit in FPGA, reducing measurement noise and improving accuracy. Future work includes large-scale testing and parameter optimization.
References
- A. M. Nascimento, P. S. Cugnasca, L. F. Vismari, J. B. Camargo Junior and J. R. de Almeida, “Enhancing the Accuracy of Parking Assistant Sensors with Bayesian Filter,” 2018 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Madrid, Spain, 2018, pp. 1-6, doi: 10.1109/ICVES.2018.8519512.
- Nascimento, A. M., et al. Research Notes on Adaptive Low-Cost Sonar Distance Sensors.